Trigonometry Explained

It looks like you've provided a comprehensive list of topics within trigonometry, vectors, complex numbers, and coordinate geometry that are commonly taught in higher mathematics courses, especially at the high school or early college level. Here's a brief overview of each topic and its significance:

Trigonometry

1. Angles and Triangles: Understanding the different types of angles (acute, obtuse, right) and triangles (right-angled, isosceles, equilateral, etc.).
2. Trigonometric Functions: Ratios of the sides of a right triangle (sine, cosine, tangent), and extensions to non-right triangles using trigonometric ratios (sine, cosine, tangent).
3. Laws of Trigonometry: The Pythagorean identity, sum and difference formulas, product to sum formulas, and half-angle formulas.
4. Inverse Trigonometric Functions: Arcsine, arccosine, arctangent, and their properties.
5. Trigonometric Equations: Solving trigonometric equations using various methods including algebraic manipulation, factoring, and inverse trigonometric functions.
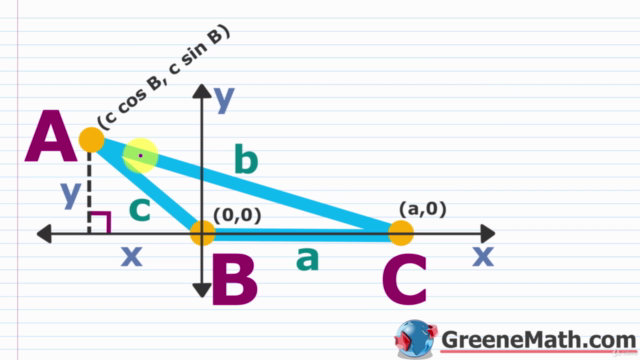
6. Law of Sines and Law of Cosines: For solving problems involving triples of angles or sides in triangles.
7. Vectors and Tripathy's Theorem: The geometry behind the distribution of raindrops or other phenomena where all directions are equally likely.

Vectors

1. Vector Basics: Definition, components, scalar multiplication, and vector addition.
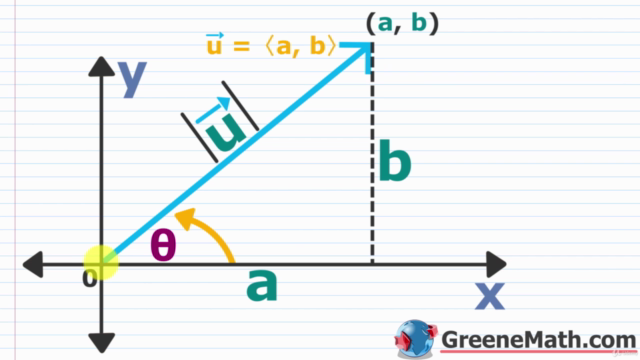
2. Magnitude of a Vector: Finding the length of a vector, which measures its size and direction.
3. Direction Angles: Finding the angles that a vector makes with the coordinate axes.
4. Vector Dot Product: A scalar value that represents the magnitudes of two vectors multiplied by the cosine of the angle between them.
5. Angle Between Vectors: The angle (in degrees or radians) between two vectors.
6. Orthogonality: Two vectors are orthogonal if their dot product is zero.
7. Complex Numbers in Vectors: Expressing a vector in terms of complex numbers for certain applications.

Complex Numbers

1. Complex Number Basics: Real and imaginary parts, notation, and arithmetic operations (addition, subtraction, multiplication, division).
2. Polar Form: Representing a complex number using magnitude and angle (radius-angle form).
3. De Moivre's Theorem: Generalizes the powers of complex numbers in polar form.
4. Roots of Complex Numbers: Finding all possible expressions for a complex number raised to a given power, typically involving polar coordinates.
5. Product and Quotient Theorems: Theorems that provide an alternative method to multiplying or dividing complex numbers in polar form.
6. Converting Between Rectangular and Polar Forms: Moving back and forth between the two representations of complex numbers.
7. Solving Equations: Solving equations involving complex numbers, using roots and other algebraic methods.

Coordinate Geometry (Rectangular and Polar Coordinates)

1. Polar Coordinate System: An alternative coordinate system that uses angle measure (theta) and distance from the origin (r) to identify a point on a plane.
2. Conversion Between Rectangular and Polar Forms: Translating coordinates between the Cartesian (rectangular) and polar systems.
3. Plotting Points in Polar Coordinates: Locating points on a coordinate grid using polar notation.
4. Graphing Lines and Circles: Drawing lines and circles on a polar plane, which is particularly useful for circles for which the equation is naturally expressed in polar form.
5. Distance Between Points: Calculating the distance between any two points, whether in rectangular or polar coordinates.
6. Inclination of a Line and Angle Between Lines: Measuring the slope or steepness of a line and the angle between two lines.

Each of these topics plays a crucial role in understanding the mathematical principles that underpin various applications in science, engineering, economics, physics, and more. Mastery of these concepts is essential for students who plan to pursue higher education in STEM fields.