التفاضل الجزئي والتكامل الثنائي والثلاثي

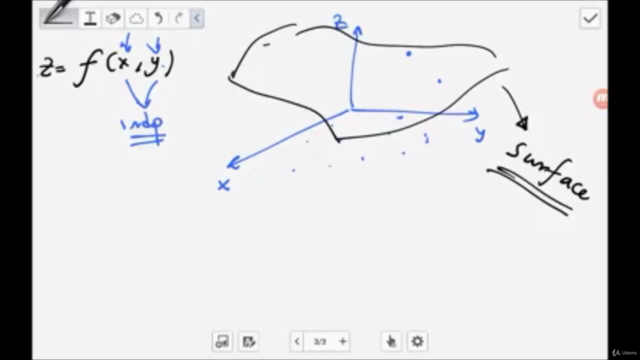
🚀 كورس الدوال ذات المتغيرات (Functions) & تكاملها: من التفاضل الجزئي إلى الثلاثي 🧮

مقدمة:

عندما نتحول إلى البرمجة، نتطلع على فهم كيفية تعبير الأفضل من الألغوهات والكذلك كيفية إجراء الإجراءات بطرق فعّالة ومؤدية. في هذا الكورس، سنلتفس بأسرار الدوال ذات المتغيرات (Functions)، ونتنوع في طرق الإجراء وتحليل البيانات. سنبدأ من الجزء الجذر للفهم، ونزيد إلى نطاق أطور حتى نواصل إلى نماذج التكامل الثلاثي.

المحتوي:

🔹 فهم الدوال ذات المتغيرات:

• أساسيات تعبير الدوال.
• مجالات الدوال وكيفية تحديدها.
• استخدام الدوال لإضافة قوة وتنظيف الكود.

🔹 التفاضل الجزئي:

• كيفية إعداد دالة تأخذ معامل وإرجاع معلومات.
• الحلقات (Loops) والتكرار النظر لدوال.
• البيانات الثابتة وإعادة الاستخدام (Parameterized Function Calls).

🔹 قاعدة السلسلة:

• كيفية بناء دالة تأخذ مجموعة من الإضرابات.
• الحفاظ على القيم المرتفعة واستخدامها بشكل فعّال.
• تطبيقات السلسلة في الألغوهات المختلفة.

🔹 التكامل الثنائي والثلاثي:

• دراسة الأحدث في التكامل (Higher-Order Functions).
• كيفية إنشاء دالة تقوم بإجراء آخرى.
• تطبيقات متعددة للتكامل (Callbacks, Events, etc.).

هدف الكورس:

أسطورًا بإمكانية تحليل وتقنية نظرًا لإجراء دالات مبتكرة وكفاء جذر، وكذلك القيام بتكامل مختلف الطرق والأسلحة لإنشاء نماذج مكونة وقاوية. ستكون مُهتمًا بكل شئ، من الأساس إلى التطورات التقدمية، وستعود في القيام بمشاريع واضحة تظهر كيفية تنظيم الألغوهات لإنتاج نتائج مقياسة وفعّالة.

ما تستند إلى الكورس؟

• تحسن مهارات برمجة لغة طريقة معينة (Functions).
• فهم بشكل عميق كيفية الإجراء الآلي (Automated Execution).
• القدرة على التحقق من الألغوهات وتحسين أدائها.
• تطوير أبلاغ قوية ومكونة لحل مشكل بأنحاء.

الأضوات:

🎓 خبرة طويلة في التعليمات والبرمجة. 👩‍💻 دالة مصقرة للتعليم وإضافة قيم. 🧠 دعم بشكل شامل ومجموعة تشمل أطفال وأسرة.

الانضمام:

إنضم إلينا اليوم وبدأ في مستوى الإبداع والتطوير! 🌟