Partial Differential Equations: Comprehensive Course

🚀 Course Title: Partial Differential Equations: Comprehensive Course

🎓 Headline: Master PDEs with Fourier Transform, Fourier Series & Separation of Variables + Uncertainty Principle Bonus Content!

👩‍🏫 Course Instructor: Emanuele Pesaresi

📚 Course Description:

Discover the elegance and power of the Fourier Transform in solving complex Partial Differential Equations (PDEs). This course meticulously explores the application of Fourier Series, Fourier Transforms, and the Separation of Variables method to solve PDEs. With an additional focus on the Uncertainty Principle, you'll gain a profound understanding that extends into the realm of quantum mechanics.

📈 What You'll Learn:

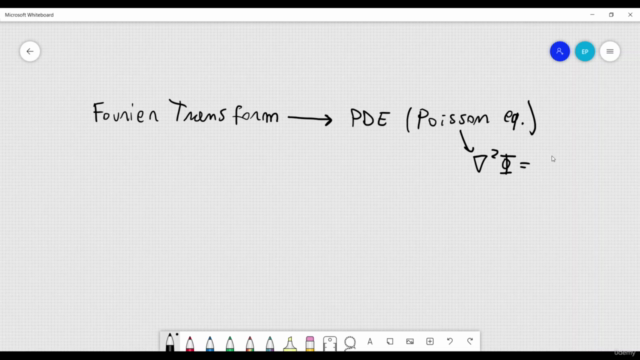
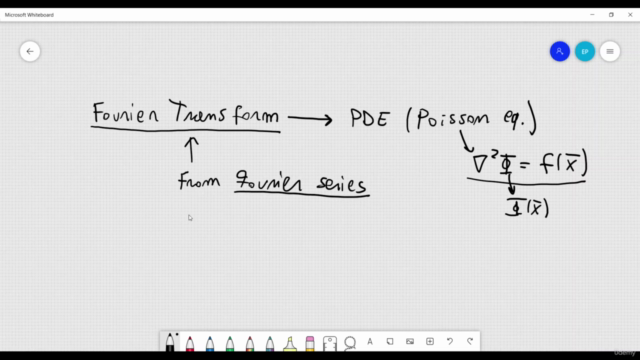
Part 1: Fourier Series and Fourier Transform Basics

• Dive into the world of Fourier Series and derive the Fourier Transform.
• Understand the inverse transformation and its significance in solving PDEs.
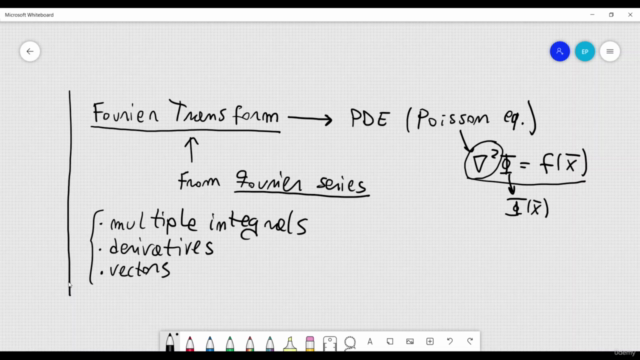
• Prerequisites: Proficiency in Calculus and Multivariable Calculus, with an emphasis on derivatives, integrals, gradient, Laplacian, and spherical coordinates.

Part 2: Solving PDEs with the Separation of Variables Method

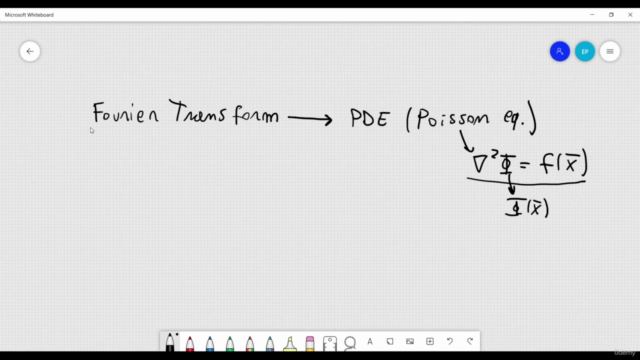
• Explore key equations like the heat equation and Laplace equation in various coordinate systems.
• Apply the Separation of Variables method to solve PDEs with diverse boundary conditions.
• Recommended prior knowledge: Understanding of Ordinary Differential Equations (ODEs).

Part 3: The Heat Equation from Physics Principles

• Derive the Diffusion/Heat equation from first principles.
• Solve the equation using a rigorous approach.
• Engage with bonus sections that delve into the mathematical underpinnings of the Heisenberg Uncertainty Principle.

🎁 Course Benefits:

• Acquire a comprehensive understanding of PDEs through the lens of Fourier Transform techniques.
• Learn to apply the Separation of Variables method effectively to solve various problems with different boundary conditions.
• Gain insights into the physical foundations of the Diffusion/Heat equation.
• Explore bonus content on the Heisenberg Uncertainty Principle, offering a peek into quantum mechanics.

📅 Prerequisites:

• Solid foundation in Calculus and Multivariable Calculus.
• Some knowledge of Complex Calculus and residues may be beneficial for a deeper grasp of certain topics.

👥 Who is this course for?

• Students and professionals with a background in Mathematics or Physics who wish to enhance their skill set in solving PDEs.
• Individuals intrigued by the mathematical principles of quantum mechanics, especially those interested in the Uncertainty Principle.

By enrolling in this course, you're not just learning a set of techniques—you're unlocking a world of mathematical beauty and physical reality. Join us on this journey through Partial Differential Equations and emerge with a newfound mastery that will propel your understanding to the next level! 🌟

👉 Sign up now and transform your approach to solving PDEs with Fourier Transforms!