線形代数の理論とPythonによる実践

了解しました。このテキストは、線形代数に関するオンライン講座の概要を提供しています。講座は以下のような内容を網羅している可能性が高いです：

1. 連立一次方程式: 問題の設定、Gauss-Jordan消去法の適用、そして幾何学的解法について説明します。

2. ベクトルと行列: ベクトルのPythonでの操作方法、行列の計算方法、行列の積について学びます。

3. 数学の基礎: 集合論、論理、写像、二項演算、群統の概念を復習します。

4. ベクトル空間: 基底、部分空間、線形写像とその行列表現について説明します。

5. 解が一意的に存在する連立方程式の解法: Gauss消去法、LU分解、PA_LU分解について学びます。

6. 解が無限に存在する連立方程式の解法: 階段行列、線形写像の核、一般行列のPA_LDU分解、Pythonを用いた解法について説明します。

7. 内積: ユークリッド空間、ピタゴラスの定理、直交性、内積と転置行列、射影、ユニタリ空間、グラム・シュミット正規直交化法について学びます。

8. 解が存在しない連立方程式の近似解法: 最小2乗法と射影、回帰分析について説明します。

9. 固有値と固有ベクトル: 線形変換、固有値問題の解法、複素共役、随伴行列、エルミート行列のスペクトル分解について学びます。

10. 行列の対角化: 相似と対角化、正規行列、フィボナッチ数列、マルコフ過程、主成分分析について説明します。

この講座は、理論と実践を結びつけることを目指しており、特にPythonを使った実践的なアプローチに焦点を当てています。コースの進め方は基礎から地道に式を追っていく形で、幾何学的解法などの概念を理解し、それをPythonコードで実装することを目指します。

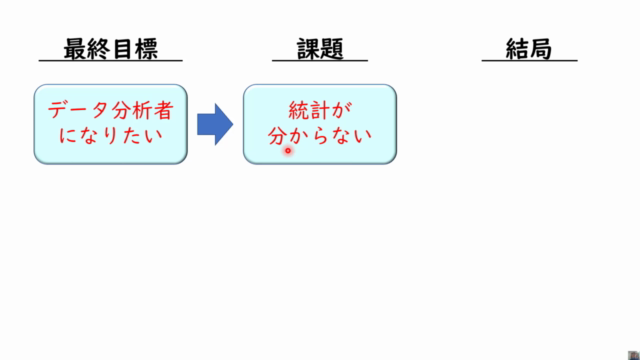
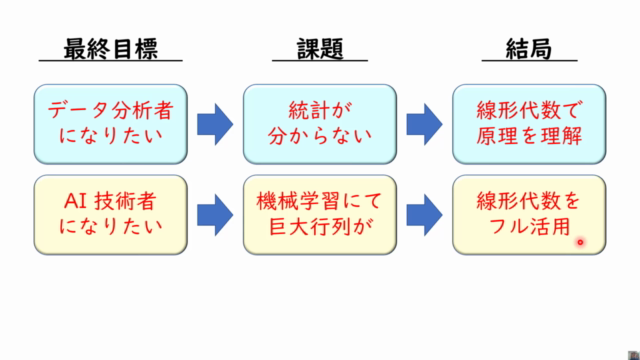
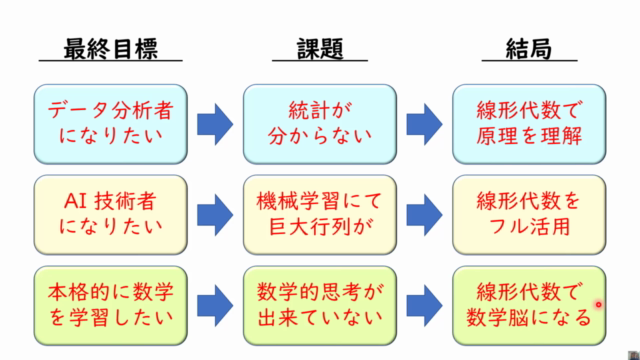
この講座は線形代数に精通したいと考えている方々に適しており、特にデータサイエンスや機械学習分野でPythonを活用することが多いため、実際のプロジェクトでの応用が容易になるでしょう。