イメージでわかる特殊相対性理論 -線形代数で導くアインシュタインの公式-：社会人になってから学ぶ数学と物理学（中級編）

🌟 アインシュタインの相対性理論を題材に線形代数の具体的な使い方が身に付くコース

コーストITLE: 「社会人になってから学ぶ数学と物理学（中級編）」 イメージでわかる特殊相対性理論 -線形代数で導くアインシュタインの公式-

コース概要

数学を「楽しい！」と感じられなかったあなたへ。

線形代数は、AIや量子コンピュータなどの最先端技術の基礎ですが、本来にそれを理解することは、抽象的な表現が苦手な方にとって難しいものだと感じていませんか？

数学を「数学だけ」で学ぶことは限界に達しているようです。そこで、物理学を通じて線形代数の奥義を探求しようとどうやったらいいのか、と悩んだ皆様へ。

このコースでは、特殊相対性理論の理解をきちんと深めながら、線形代数の魅力を体験します。

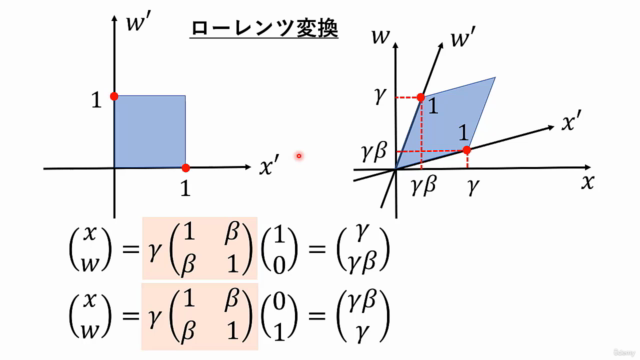
ベクトルや行列を使って計算を進めることで、時間と空間の驚くべき性質をイメージしやすくなります。これにより、数式E=mc2や時間の遅れ、ローレンツ収縮などアインシュタインの公式が、自分の手で解明されると聞くことでしょう。

コース内容

• 特殊相対性理論の基本概念と物理的な背景から始めます。
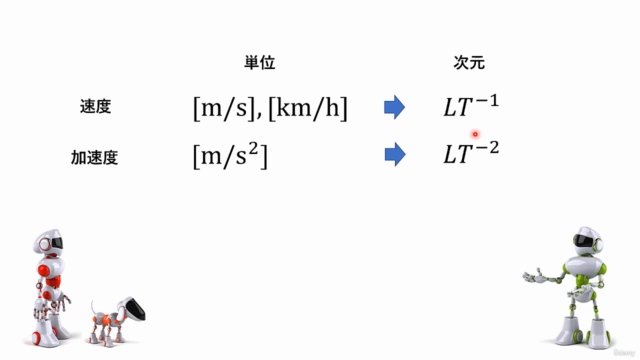
• 線形代数の基本手段、ベクトル、行列の使い方を学びます。
• 数式E=mc2の導出を通じて、エネルギーと物質の関係を理解します。
• 時間の遅れやローレンツ収縫などの相対性効果を、実際の計算で検証していきます。
• コースの終わりには、課題と Practical Exercisesで新たに学んだ知識を駆使します。

学習メリット

• 物理学を通じた数学の理解: 抽象的な概念だけでなく、実際の物理現象を解明することで、線形代数の意義と応用が明確になります。
• 現代科学の基礎知識: テクノロジーが進化するある時代で、科学的な理解を持つことで、より深い洞察力を身につけることができます。
• 数学技術の向上: 行列とベクトルを使った計算能力が向上し、他の科学的分野や技術分野でも役立ちます。

ターゲットとなる皆様

• 数学が苦手だけでなく、物理学に関心のある方々
• テクノロジー分野で働く方々 who wants to understand the background science of their work
• 科学的な知識を深めたい and curious individuals

受講のメリット

• 数学と物理学のブリッジ: 2つの分野の間で橋渡しすることで、新たな視点から科学を理解することができます。
• 実践的なスキル: 実際の計算や問題解決を通じて、線形代数の知識を駆使することができます。
• 知識の広がり: 特殊相対性理論の外側から一歩飛び出し、より幅広い知識領域にアクセスしやすくなります。

数学と物理学を楽しむ旅は、このコースから始めてみませんか？それでは、今日からただ一歩疑問から立ち出し、新たな知識への道を探求しましょう！

注: このコースの内容や進め方は、教育者や学習者のニーズに応じて柔軟に変更する可能性があります。最新のカリキュラムと資料は、コース開始前に確認してください。