Calculus 3 (multivariable calculus), part 2 of 2

🎓 Course Title: Calculus 3 (Multivariable Calculus) - Part 2 of 2

Overview of Calculus 3, Part 2

Towards and through the Vector Fields
📚 Based on chapters from Robert A. Adams & Christopher Essex' "Calculus: A Complete Course" (8th or 9th edition)

Course Structure

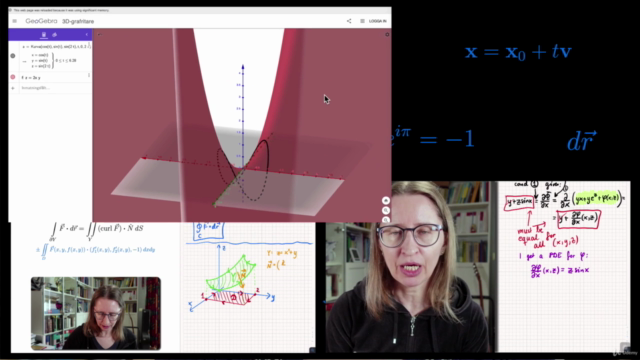
Chapter 14: Multiple Integrals

• S1. Introduction to Multiple Integrals

  • Overview of the chapter and what to expect.

• S2. Repetition (Riemann integrals, sets in the plane, curves)

  • Solidifying foundational concepts before moving forward.

• S3. Double Integrals

  • Computing double integrals over APR using iteration.
  • Understanding x-simple and y-simple domains.
  • Iteration of double integrals through Fubini's theorem.

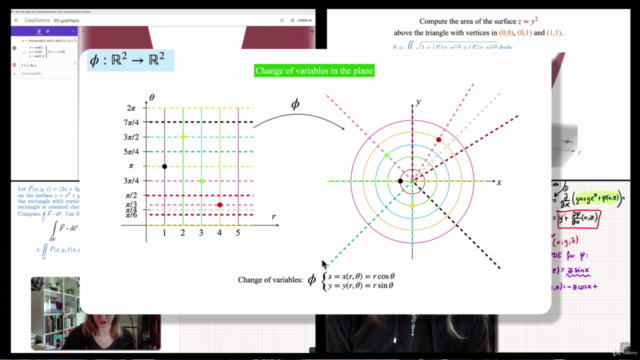
• S4. Change of Variables in Double Integrals

  • Learning to compute double integrals via polar coordinates and other substitutions.

• S5. Improper Integrals

  • Identifying convergence or divergence of improper integrals.
  • Using the mean-value theorem for double integrals to find mean values.

• S6. Triple Integrals

  • Introducing the concept of triple integration and its applications.

• S7. Change of Variables in Triple Integrals

  • Computing triple integrals using spherical or cylindrical coordinates.
  • Understanding the Jacobian for various change of variables.

• S8. Applications of Multiple Integrals

  • Applying multiple integrals to compute mass, surface area, and find the mass center.

Chapter 15: Vector Fields

• S9. Vector Fields

  • Exploring vector fields in the plane and in space.

• S10. Conservative Vector Fields

  • Understanding conservative vector fields and their properties.
  • Learning to compute potential functions for conservative vector fields.

• S11. Line Integrals of Functions

  • Calculating line integrals for various applications such as mass, arc length, and work.

• S12. Line Integrals of Vector Fields

  • Mastering three methods to compute line integrals of vector fields.

• S13. Surfaces

  • Learning about surfaces in two and three dimensions.
  • Identifying closed surfaces, understanding their boundaries, and determining normal vectors.

• S14. Surface Integrals

  • Calculating surface integrals for applications like heat transfer.

• S15. Wrap-up Multivariable Calculus / Calculus 3, Part 2 of 2

  • Summarizing the key concepts learned in this course.

Chapter 16: Vector Calculus and Advanced Topics

• S16. Gradient, Divergence, and Curl

  • Defining and computing gradient, divergence, and curl for vector fields.

• S17. Green's Theorem

  • Understanding Green's Theorem as a connection between line integrals and surface integrals.

• S18. Gauss's Theorem (Divergence Theorem)

  • Applying Gauss's Theorem to convert volume integrals into surface integrals.

• S19. Stokes' Theorem

  • Learning how Stokes' Theorem relates the contour integral of a closed loop to the flux through the bounded surface spanning that loop.

• S20. Extras

  • Exploring additional resources and potential future courses.

Important Notes

• Professor's Guidance: Always check with your professor which parts of the course are relevant to your final exam, as requirements can vary.

• Comprehensive Material: A detailed outline of all videos and their titles, along with solved problems, is provided in the resource file "001 Outline_Calculus3_part2.pdf" (located under video 1, "Introduction to the course"). This material also covers topics in depth.

• Stay Updated: Keep an eye on our offerings for upcoming courses and hypothetical release dates.

Dive into the fascinating world of multivariable calculus with this comprehensive course, where you'll master the intricacies of multiple integrals, vector fields, and their applications. Embark on this mathematical adventure today! 🧮🚀